Concepto de árbol
Serie “Árboles, árboles binarios y árboles ordenados”
Este es el artículo número 1 de la serie “Árboles, árboles binarios y árboles ordenados”:
Cuando pensamos un árbol en el mundo real, nuestro concepto incluye el tronco, ramas, hojas y raíces. En esta idea imaginamos que tanto las ramas como las hojas parten del tronco como un producto de este de forma jerárquica o con una relación de dependencia.
Hay ciertos tipos de datos que manejan esta relación de jerarquía para expresar sus características particulares, de acuerdo al contexto donde se aplican. Una forma de definir un árbol en programación sería la siguiente:
Definición de árbol
Son un estructuras de datos, formadas por nodos y enlaces, que guardan información sobre los nodos anteriores y posteriores.
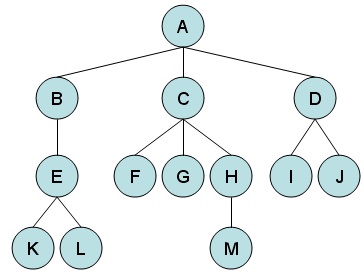
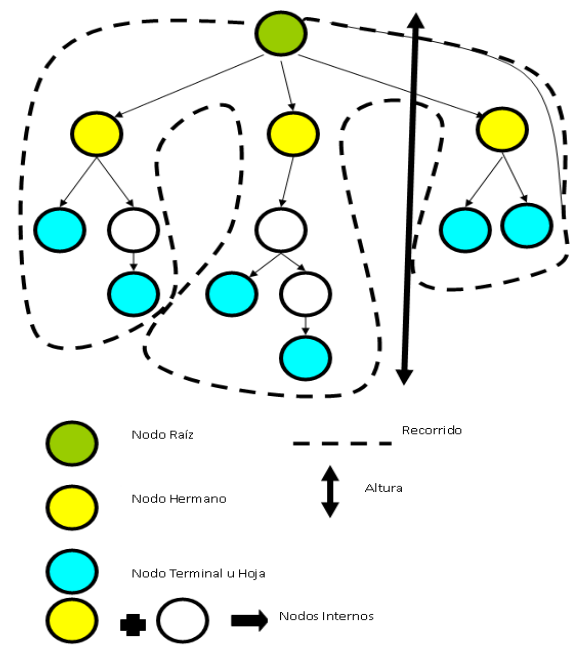
Aplicaciones de los árboles
- Los árboles son utilizados en algoritmos de ordenación, clasificación y búsqueda.
- En el desarrollo de compiladores, los árboles se utilizan para representar expresiones de sintaxis del lenguaje de programación.
- En inteligencia artificial, los árboles se utilizan para programación de toma de decisiones, árboles de juegos, árboles de resolución, etc.
Estructura de un árbol
- Nodo raíz (root)
- Es el elemento principal del árbol y de él parten el resto de los nodos; es el único nodo sin nodo padre.
- Nodo (node)
Son cada uno de los elementos que forman el árbol y se enlistan a continuación.
- Nodo hijo (child): Nodo que descienden de otro nodo.
- Nodo padre (parent): Nodo que antecede a otro nodo. Todos los nodos tienen un solo padre, excepto el raíz.
- Nodo terminal u hoja (leaf): No que no tiene hijos (se encuentra al final del camino).
- Nodo interior (internal node): Nodos que no son hojas ni raíz.
- Hermanos (siblings): Un grupo de nodos con el mismo padre.
- Arista (edge)
- Conexión entre dos nodos.
- Camino o recorrido (path)
- La secuencia de nodos y aristas que conectan a un nodo con un descendiente.
- Nivel (level)
- Número de conexiones que se tiene desde la raíz a un nodo específico.
- Rama (branch)
- Aristas entre nodos que termina en una hoja.
- Altura o profundidad (depth)
- Número máximo de nodos en una rama.
Definición del tipo de dato abstracto árbol binario
Un árbol binario, representado como T, se define como un conjunto finito de elementos llamados nodos, de forma que:
- Si T está vacío, se llama árbol nulo o árbol vacío.
- T contiene un nodo distinguido, que llamaremos R, y que es la raíz de T.
- Los restantes nodos de T forman un par ordenado de árboles binarios separados T1 y T2.
- Si T contiene una raíz R, los dos árboles T1 y T2 se llaman, respectivamente, sub-árboles izquierdo y derecho de la raíz R.
- Si T1 no está vacío, entonces su raíz se llama sucesor izquierdo de R; y análogamente, si T2 no está vacío, su raíz se llama sucesor derecho de R.
La siguiente imagen te muestra cómo se representa un árbol binario en la estructura de datos, en la que puedes observar que:
- B es un sucesor izquierdo y C un sucesor derecho del nodo A.
- El subárbol izquierdo de la raíz A consiste en los nodos B, D y E, y el subárbol derecho de A consiste en los nodos C, F y G.
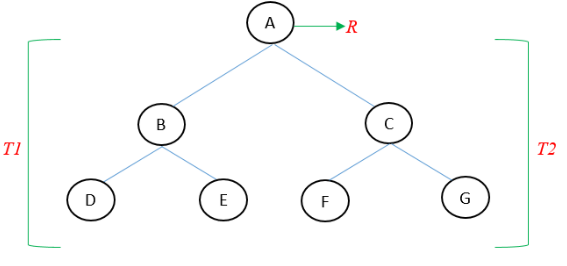
Otras características que podemos deducir del árbol T son:
- T es recursiva, ya que T se define en términos de los sub-árboles binarios T1 (nodos B, D y E) y T2 (nodos C, F y G). Esto significa, en particular, que cada nodo (que llamaremos N de T) contiene un sub-árbol izquierdo y uno derecho. Además, si N es un nodo terminal, ambos árboles están vacíos.
- Dos árboles binarios T y T’ se dicen que son similares si tienen la misma estructura o, en otras palabras, si tienen la misma forma. Los árboles se dice que son copias si son similares y tienen los mismos contenidos en sus correspondientes nodos.
Representación
Un árbol binario se puede representar por medio de datos tipo puntero 9que veremos en esta serie) y por medio de arreglos. Cada representación es un registro de datos que contiene por lo menos tres campos:
- Uno que almacena la información del nodo.
- Otro que señala el árbol izquierdo del nodo actual.
- Un tercero que indica al árbol derecho del nodo actual.
Ejemplo
Por ejemplo, consideremos un árbol binario que representa la expresión matemática 1 * ((3 ^ 4) + 2). Su representación en memoria sería la siguiente:
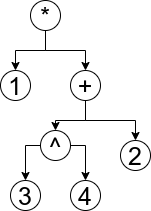
Ahora, si cada registro tiene tres campos, entonces esta misma expresión se vería así como un árbol binario:
