Cómo crear un árbol binario de expresiones

Seguimos con nuestro programa sobre árboles binarios para crear y evaluar la expresión $1\times((3^4)+2)$. Pero primero vamos a definir árbol binario.

Un árbol binario es un árbol (estructura idealmente no lineal) de orden dos, es decir que solo puede tener dos ramas.

Una característica importante de un árbol binario de estructuras es que tienen un orden y debemos comprenderlo para formar correctamente nuestras expresiones.

Estructura de una expresión

Lo primero es que la expresión debe estar balanceada, debe
tener tres partes, el nodo, un enlace a la izquierda y un
enlace a la derecha. Las excepciones son el nodo raíz, un
árbol vacío y las hojas.

Podemos balancear un árbol usando paréntesis. En nuestro caso,
identificamos las tres partes así:

Ahora, con estos elementos, formaremos el primer nivel de
nuestro árbol binario de la expresión, marcando como nodo
raíz, el operador al centro.

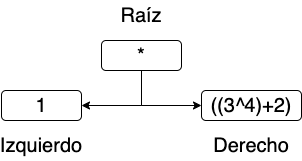
Vemos que en la rama derecha hay una expresión que está
balanceada por lo que podemos convertir en el siguiente nivel
de nuestro árbol.

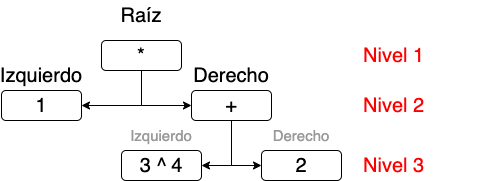
Nuevamente, vemos que en el lado izquierdo del tercer nivel
hay una expresión balanceada que debemos expresar como un
nuevo nivel o sub-árbol.

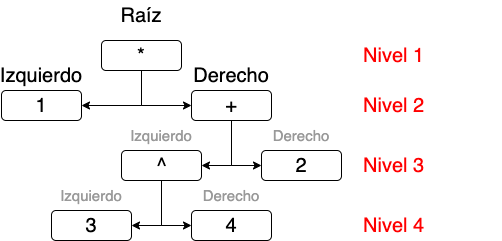
Y así es como debemos construir el árbol para nuestra
expresión.

Construcción de un árbol de expresiones

Observemos entonces que en un árbol de expresiones debemos indicar explícitamente el nodo izquierdo y el nodo derecho. Empecemos definiendo la estructura del árbol.

#include <stdio.h>
#include <stdlib.h>

// Estructura del árbol binario
typedef struct node {
  char data;
  struct node* left;
  struct node* right;
} BinaryTree;

A continuación, definimos los prototipos de las funciones que vamos a utilizar.

BinaryTree* getNode(char data);
BinaryTree* insertLeft(BinaryTree* node, char data);
BinaryTree* insertRight(BinaryTree* node, char data);
void preOrder(BinaryTree* node);
void inOrder(BinaryTree* node);
void postOrder(BinaryTree* node);

La función getNode() toma un nodo y le asigna un valor a la variable data.

BinaryTree* getNode(char data) {
  BinaryTree* node = (BinaryTree*)malloc(sizeof(BinaryTree));
  node->data = data;
  node->left = NULL;
  node->right = NULL;
  return node;
}

Las siguientes funciones son las más importantes para nuestro árbol binario de expresiones. insertLeft e insertRight agregan un nuevo nivel a nuestro árbol.

BinaryTree* insertLeft(BinaryTree* parent, char data) {
  parent->left = getNode(data);
  return parent->left;
}

BinaryTree* insertRight(BinaryTree* parent, char data) {
  parent->right = getNode(data);
  return parent->right;
}

La función inOrder() recorre nuestro árbol en el orden que definimos nuestra expresión.

void inOrder(BinaryTree* root) {
  if (root == NULL) {
    return;
  }
  inOrder(root->left);
  printf("%c ", root->data);
  inOrder(root->right);
}

Definición de la expresión en el árbol binario

Definir una expresión en nuestro árbol tiene una peculiaridad: indicamos el nodo dentro del nodo, para indicar el nivel.

int main() {
  BinaryTree* root = getNode('*');   // Raíz

  insertLeft(root, '1');    // Rama izquierda, nivel 1
  insertRight(root, '+');   // Rama derecha, nivel 1

  insertLeft(root->right, '^');  // Rama izquierda, nivel 2
  insertLeft(root->right->left, '3');  // Rama izquierda de la rama izquierda, nivel 3
  insertRight(root->right->left, '4'); // Rama derecha de la rama izquierda, nivel 3

  insertRight(root->right, '2');
  
  printf("In-order: ");
  inOrder(root);
  
  return 0;
}